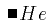 .[Cajori, 1928/1929]
.[Cajori, 1928/1929]Working Draft 10-Jul-1997
As has been noted in the introductory sections of this report, Mathematics can be distinguished by its use of a (relatively) formal language, mathematical notation. Mathematics and its notation should not be viewed as one and the same thing. The intent of content markup in Mathematical Markup Language is to support the encoding of underlying mathematical content of an expression, rather than any particular rendering for the expression.
For example the construct "H multiplied by e" is expressed using an explicit operator H<TIMES/>e. In different presentational contexts, the multiplication operator might be invisible (e.g. on paper), or rendered as the spoken word "times". Knowing the underlying mathematical construct, it is often possible to generate many different presentations according to the context and style preferences of the author or reader. For common expressions a default visual presentation is usually clear. "Take care of the sense and the sounds will take care of themselves" wrote Lewis Carroll [Carroll 1871]. Going in the reverse direction, that is from a presentation form to the underlying construct, is not necessarily easy: "He" could be interpreted as an atomic text string (or a chemical symbol). Context information may be required to decide between possible interpretations. Clues as to the interpretation are plainly important to speech rendering.
Mathematical presentation changes with culture and time: some
expressions in combinatorial mathematics today would have one meaning
to an English mathematician, and quite another to a French
mathematician. Notations may lose currency, for example the use of
musical sharp and flat symbols to denote maxima and minima. [Chaudry 1954] A notation in use in 1644 for the
multiplication mentioned above was 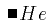 .[Cajori, 1928/1929]
.[Cajori, 1928/1929]
Encoding the underlying mathematical constructs allows us to interchange information more precisely with systems which are able to manipulate the mathematics. In the trivial example above, such a system could substitute values for the variables H and e, evaluating the result. Further interesting application areas include CD-based textbooks and other interactive teaching aids.
It is clear that the semantics of much mathematical notation is not yet a matter of consensus. In any case it would be an enormous job to codify most of mathematics, and indeed a task which could never be complete. Therefore this MathML proposal specifies a number of commonplace mathematical constructs which should be useful to a large number of potential users. The content tags set out below should be adequate for simple coding of most of the formulas used from kindergarten to the end of high school in the US, and probably beyond through the first two years of college, that is up to A-Level or Baccalaureat level.
The areas covered to some extent in this initial draft are:
It is not claimed, or even suggested, that the proposed element set is complete for these areas.
The guidelines governing the design of the MathML content elements are the following principles:
In order to accomplish these goals, MathML introduces two types of Content elements. The first type typically represents operators and functions, such as <SIN/> and <PLUS/>. These elements are canonically empty. Operators and functions are applied to arguments by using another empty element, the <APPLY/> element.
Elements of the second type can be seen as containers, and in general serve to mark the scope of the operators contained in them, or to define a context for the elements contained. Examples of this type are the mathematical expression construct <EXPR>, and <SET> .
MathML content tags directly encode the mathematical meaning of expressions, but this does not of itself define the notation used to present the meaning to a reader. Default visual renderings for the content elements are given in Section 4.2 . In addition, content tags , in common with all MathML tags, have a "STYLE" attribute (see Section 4.4), which can be used to pass rendering preference information on to a specific renderer which can make use of it.
The basic building block of a mathematical expression in MathML content markup is the EXPR element. An EXPR corresponds to a complete mathematical expression. Roughly speaking, this means a piece of mathematics which could be surrounded by parentheses or "logical brackets" without changing its meaning.
For example,
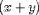 might be encoded as
might be encoded as
<EXPR> <MI>x</MI> <PLUS/> <MI>y</MI> </EXPR>.
Using EXPR, (as with braces in traditional mathematics notation), it is possible to specify exactly the scope of any operator or function. The content model of EXPR is simple and recursive. Symbolically, the content model can the described as:
EXPR => a op b
where a and b are simple identifiers, or EXPR constructs
themselves, and op is any operator or function.
Note that this allows EXPR constructs to be nested to
arbitrary depth.
An EXPR may also optionally contain more than one operator:
EXPR => a op b [op c ...]
For example,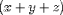 can be encoded as
can be encoded as
<EXPR> <MI>x</MI> <PLUS/> <MI>y</MI> <PLUS/> <MI>z</MI>
</EXPR>.
When an EXPR is used in this way, it is important to keep in mind
the issue of operator precedence. In cases where several operators
are enclosed in a single EXPR, operator association or precedence must
be resolved by an external processing application, if it wishes to
evaluate the EXPR. Therefore, in most situations, it is probably
preferable to fully bracket expressions, particularly when several
different operators are involved. For example, 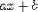 is better encoded as
is better encoded as
although it is also valid to encode it as<EXPR> <EXPR><MI>a</MI><TIMES/><MI>x</MI></EXPR> <PLUS/> <MI>b</MI> </EXPR>
<EXPR><MI>a</MI><TIMES/><MI>x</MI><PLUS/><MI>b</MI></EXPR>.
In addition to determining the scope of operators and functions, the <EXPR> container plays an important role in grouping expressions within other constructs. For example, by default a <VECTOR> element expects to have its components separated by an explicit separator, the <SEP/> tag. However, an expression enclosed by an EXPR is viewed as a single coherent molecule, so that the <SEP/> tag is not needed to separate it from its neighbors.
Since the bracketing is logical, it need not necessarily be rendered. Default rendering.
One reason for using MathML content markup is to make the
mathematical expressions easily available to external processing
applications such as computer algebra systems, and intelligent
renderers. Therefore, a key requirement of functional representation
in content markup is that it must be possible to perform symbolic
algebra on mathematical functions as first class objects, and
apply the result to an argument. That is, in addition to
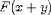 we must be able to encode
we must be able to encode
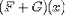 .
.
To understand the MathML approach to applying a function to an argument, consider f(x). This can be encoded as
<EXPR> <MI>f</MI> <APPLY/> <MI>x</MI> </EXPR>
Note that f and x may be simple identifiers, or more
complex constructs built from EXPRs and other function elements.
For example, one can construct 'new' functions which can then be
applied to an argument using the APPLY element. Thus, the expression
(F + G)-1(x) can be encoded as
<EXPR>
<EXPR>
<INVERSE/>
<APPLY/>
<EXPR><MI>F</MI><PLUS/><MI>G</MI></EXPR>
</EXPR>
<APPLY/>
<MI>x</MI>
</EXPR>
Functions supported explicitly in MathML are all canonically empty elements and can be used as first class objects in symbolic manipulation. Examples are <PLUS/>, <SIN/>. User defined functions such as <FN>functionname</FN> can also be used in this way. Although, it is probably best to always use the APPLY element, just as it is prudent to fully bracket expressions with EXPRs, the APPLY element is optional and may be omitted in unambiguous situations. The only such situation which commonly arises is when a function named in MathML appears alone with an argument in an EXPR. For example, we can write sin (x) as
<EXPR><SIN/> <MI>x</MI> </EXPR>
as there is no other operator within the EXPR.
Default rendering of APPLY.
The INVERSE construct is problematic from a mathematical point of view in that it implicitly involves the definition of an inverse for an arbitrary function F. Even at the K through 12 level the concept of an inverse F-1 of many common functions F is not used in a uniform way. For example, inverse trigonometric functions are inverses in a slightly different way from the way in which log function is the inverse of the exponential.
In an effort to be as inclusive as possible, MathML adopts the view that
"If F is a function from a domain D to D', then the inverse G of F is a function over D' such that G(F(x)) = x for x in D."This definition does not assert that such an inverse exists for all or indeed any x in D, or that it is single-valued anywhere. Authors writing pedagogical material that may be evaluated by other applications may therefore wish to address the issue of the existence of a particular inverse function.
In order to simplify processing of MathML by rendering applications, MathML includes a concept called "leaf-tagging". This means that, at the lowest level, any PCDATA token is encapsulated in an element defining its presentation type. For reasons of simplicity, Content Markup uses the token tags from the Presentation Tagset: MI and MN are used to encapsulate identifiers and numbers. MF and MTEXT may also be used to encapsulate fences and embedded text. This type information is intended for renderers and may be ignored by mathematical processing applications.
This is the simplest form of embedded presentation markup. Presentation constructs of arbitrary complexity may be embedded in place of the simple tokens MI, MN etc. This is discussed in more detail in section 5.
The MathML content tags are given in tables below. They are grouped in categories which roughly reflect the area of mathematics from which they come, and also the grouping in the MathML DTD.
There is no linguistic difference in MathML between operators and functions. The separation here and in the DTD is for reasons of clarity. Some functions in this list may not ever be used in symbolic manipulations.
| Tag | Description | Default Rendering |
|---|---|---|
| <APPLY/> | makes explicit application of a function to its argument | By default, the APPLY element renders as a thin space between the function and its argument, or as the spoken word "of". Note that this does not automatically create the parentheses around the function argument. Rendering Notes |
| <E> | equation or relation (see notes) |
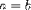
|
| <EXPR> | "scoping" or "bracketing" element | Since the bracketing is logical, it need not necessarily be rendered visually. By default, an EXPR is rendered in the same manner as the MROW presentation schema. Rendering Notes |
| <FN> | user-defined function; (see notes)<FN><MI>functionname </MI> </FN> |
|
| <INTERVAL> | interval constructor; (see notes)<INTERVAL CLOSURE="Open-Closed"> <MI>a</MI><SEP/><MI>b</MI> </INTERVAL> |
![$(a , b]$](section4_8.gif)
|
| <INVERSE/> | generic inverse for functions | |
| <SEP/> | generic separator; (see notes) | none Rendering Notes |
| <ST/> | "such that" separator; (see notes)
<SET>
<MI>i</MI> <ST/>
<E>
<MN>1</MN><LE/><
MI>i</MI><LE/><MI>n</MI>
</E>
</SET>
|
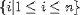
|
<E>
<MI>x</MI> <LT/> <MN>2</MN>
<ST/>
<E>
<MI>x</MI> <IN/> <MI>R</MI>
</E>
</E>
<SEP/> is a more generic separator for array-like
containers, and elements such as the INTERVAL container.| Tag | Description | Default Rendering |
|---|---|---|
| <PLUS/> | addition |
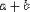
|
| <MINUS/> | subtraction |
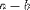
|
| <TIMES/> | multiplication |
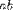
|
| <OVER/> | division |
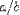
|
| <EXP/> | "exponentiation"<EXPR><EXP/><APPLY/><MI>x</MI></EXPR> |
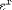
|
| <POWER/> | "to the power of"<EXPR><MI>x</MI><POWER/><MN>3</MN></EXPR> |
|
| <DIV/> | "division modulo base"<EXPR><MI>a</MI><DIV/><MI>N</MI></EXPR> |
|
| <REM/> | "remainder modulo base"<EXPR><MI>a</MI><REM/><MN>N</MN></EXPR> |
|
| <FACTORIAL> | factorial<FACTORIAL><MI>n</MI></FACTORIAL> |
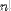
|
| <MIN> | minimum<MIN><MI>A</MI></MIN> |
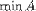
|
| <MIN> | minimum
<MIN>
<MI>x</MI> <ST/><MI>x</MI> <IN/>
<SET>
<MI>x</MI> <ST/>
<E>
<EXPR><MI>x</MI><POWER><MN>3<MN></EXPR>
<LT/>
<MI>Π</MI>
</E>
</SET>
</MIN>
|
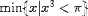
|
| <MAX> | maximum<MAX><MI>A</MI></MAX> |
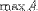
|
| Tag | Description | Default Rendering |
|---|---|---|
| <EQ/> | equals |
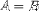
|
<E><MI>A</MI><EQ/><MI>B</MI></E> |
||
| <NEQ/> | not equal |
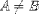
|
<E><MI>A</MI><NEQ/><MI>B</MI></E> |
||
| <GT/> | greater than |
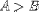
|
<E><MI>A</MI><GT/><MI>B</MI></E> |
||
| <LT/> | less than |
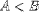
|
<E><MI>A</MI><LT/><MI>B</MI></E> |
||
| <GEQ/> | greater than or equal |
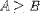
|
<E><MI>A</MI><GEQ/><MI>B</MI></E> |
||
| <LEQ/> | less than or equal |
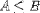
|
<E><MI>A</MI><LEQ/><MI>B</MI></E> |
| Tag | Description | Default Rendering |
|---|---|---|
| <LN> | natural logarithm |
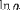
|
<LN><MI>a</MI></LN> |
||
| <LOG> | logarithm; |
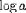
|
<LOG><MI>a</MI></LOG> |
||
| use <DEGREE> for base; (see notes) |
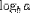
|
|
<LOG> <MI>a</MI> <DEGREE><MI>b</MI></DEGREE> </LOG> |
||
| <INT/> | one-dimensional definite integral (see notes) |
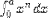
|
<EXPR>
<INT/>
<LOWLIMIT><MN>0</MN></LOWLIMIT>
<UPLIMIT><MI>a</MI></UPLIMIT>
<EXPR>
<MI>x</MI><POWER/><MI>n</MI>
</EXPR>
<BVAR><MI>x</MI></BVAR>
</EXPR>
|
By default, the upper and lower limits are rendered in their usual positions, and the bound variable is rendered with a small space and the letter "d" in front of it. | |
| <DIFF/> | derivative, differentiation |
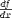
|
<EXPR> <DIFF/> <MI>f</MI> <BVAR><MI>x</MI></BVAR> </EXPR> |
||
| <PARTIALDIFF/> | partial derivative |
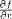
|
<EXPR>
<PARTIALDIFF/>
<MI>f</MI>
<BVAR>x</BVAR>
</EXPR>
|
||
| <TOTALDIFF/> | total derivative |
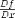
|
<EXPR>
<TOTALDIFF/>
<MI>f</MI>
<BVAR><MI>x</MI></BVAR>
</EXPR>
|
||
| <LOWLIMIT> | lower limit of integral, see notes | see <INT> |
| <UPLIMIT> | upper limit of integral, see notes | see <INT> |
| <BVAR> | bound variable; (see notes) | |
| <DEGREE> | holds the n in "nth derivative"; (see notes) |
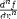
|
<EXPR>
<DIFF/>
<MI>f</MI>
<BVAR><MI>x</MI></BVAR>
<DEGREE><MI>n</MI></DEGREE>
</EXPR>
|
| Tag | Description | Default Rendering |
|---|---|---|
| <SET> | set |
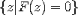
|
<SET>
<MI>z</MI><ST/>
<E>
<EXPR>
<FN><MI>F</MI></FN><APPLY/><MI>z</MI>
</EXPR>
<EQ/><MN>0</MN>
</E>
</SET>
|
||
| <UNION/> | union (join) |
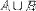
|
<EXPR> <MI>A </MI> <UNION/> <MI>B</MI> </EXPR> |
||
| <INTERSECT/> | intersection (meet) |
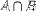
|
<EXPR> <MI>A</MI> <INTERSECTION/> <MI>B</MI> </EXPR> |
||
| <IN/> | is in, or is an element of a set |
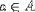
|
<EXPR> <MI>a</MI> <IN/> <MI>A</MI> </EXPR> |
||
| <NOTIN/> | is not in |
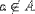
|
<EXPR> <MI>a</MI> <NOTIN/> <MI>A</MI> </EXPR> |
||
| <SUBSET/> | is a subset |
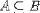
|
<EXPR> <MI>A</MI> <SUBSET/> <MI>B</MI> </EXPR> |
||
| <PRSUBSET/> | is a proper subset |
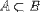
|
<EXPR> <MI>a</MI> <PRSUBSET/> <MI>A</MI> </EXPR> |
||
| <NOTPRSUBSET/> | is not a proper subset |
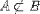
|
<EXPR> <MI>a</MI> <NOTPRSUBSET/> <MI>A</MI> </EXPR> |
| Tag | Description | Default Rendering |
|---|---|---|
| <SUM/> | sum; (see notes) |
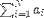
|
<EXPR>
<SUM/>
<LOWLIMIT><MN>1</MN></LOWLIMIT>
<UPLIMIT><MI>N</MI></UPLIMIT>
<BVAR><MI>i</MI></BVAR>
<EXPR>
<MSUB>
<MI>a</MI>
<MI>i</MI>
</MSUB>
</EXPR>
</EXPR> |
||
| <PRODUCT/> | product; (see notes) |
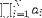
|
<EXPR>
<PRODUCT/>
<LOWLIMIT><MN>1</MN></LOWLIMIT>
<UPLIMIT><MI>N</MI></UPLIMIT>
<BVAR><MI>i</MI></BVAR>
<EXPR>
<MSUB>
<MI>a</MI>
<MI>i</MI>
</MSUB>
</EXPR>
</EXPR> |
||
| <LIMIT/> | limit; (see notes) |
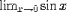
|
<EXPR> <LIMIT/> <LOWLIMIT><MI>x</MI><TENDSTO/><MN>0</MN></LOWLIMIT> <EXPR><SIN/><MI>x</MI></EXPR> </EXPR> |
||
| <TENDSTO/> | tends to |
We just list the names of the common functions provided: their interpretations should be clear.
| <SIN/> | <COS/> | <TAN/> |
| <SEC/> | <COSEC/> | <COTAN/> |
| <SINH/> | <COSH/> | <TANH/> |
| <SECH/> | <COSECH/> | <COTANH/> |
| <ARCSIN/> | <ARCCOS/> | <ARCTAN/> |
| Tag | Description | Default Rendering |
|---|---|---|
| <MEAN> | mean or average |
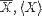
|
<MEAN><MI>X</MI></MEAN> |
||
| <SDEV> | standard deviation |
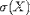
|
<SDEV><MI>X</MI></SDEV> |
||
| <VAR> | variance |
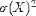
|
<VAR><MI>X</MI></VAR> |
||
| <MEDIAN> | median |
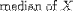
|
<MEDIAN><MI>X</MI></MEDIAN> |
||
| <MODE> | mode |
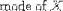
|
<MODE><MI>X</MI></MODE> |
||
| <MOMENT> | use <DEGREE> for the n in "nth moment" |
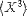
|
<MOMENT> <MI>X</MI> <DEGREE><MN>3</MN><DEGREE> </MOMENT> |
| Tag | Description | Default Rendering |
|---|---|---|
| <VECTOR> | vector; see notes |
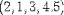
|
<VECTOR> <MN>2</MN><SEP/><MN>1</MN> <SEP/><MN>3</MN><SEP/><MN>4.5</MN> </VECTOR> |
||
| .. or.. | ||
<VECTOR> <MN>2</MN><MN>1</MN> <MN>3</MN><MN>4.5</MN> </VECTOR> |
||
| <MATRIX> | matrix | |
| <MATRIXROW> | matrix row; see notes |
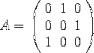
|
<E>
<MI>A</MI><EQ/>
<MATRIX>
<MATRIXROW>
<MN>0</MN><SEP/>
<MN>1</MN><SEP/><MN>0</MN>
</MATRIXROW>
<MATRIXROW>
<MN>0</MN><SEP/>
<MN>0</MN><SEP/><MN>1</MN>
</MATRIXROW>
<MATRIXROW>
<MN>1</MN><SEP/>
<MN>0</MN><SEP/><MN>0</MN>
</MATRIXROW>
</MATRIX>
</E> |
||
| .. or.. | ||
<E>
<MI>A</MI><EQ/>
<MATRIX>
<MATRIXROW>
<MN>0</MN><MN>1</MN><MN>0</MN>
</MATRIXROW>
<MATRIXROW>
<MN>0</MN><MN>0</MN><MN>1</MN>
</MATRIXROW>
<MATRIXROW>
<MN>1</MN><MN>0</MN><MN>0</MN>
</MATRIXROW>
</MATRIX>
</E> |
||
| <MATRIXINVERSE> | matrix inverse |
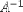
|
<MATRIXINVERSE><MI>A</MI></MATRIXINVERSE> |
||
| <DETERMINANT> | determinant |
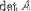
|
<DETERMINANT><MI>A</MI></DETERMINANT> |
The use of the semantic mapping elements is explained in section 4.3.
| Tag | Description | Default Rendering |
|---|---|---|
| <ANNOTATION> | container element for a semantic annotation in a non-XML format | None |
| <SEMANTICS> | container element for a MathML construct together with its semantic mapping information | None |
| <XML-ANNOTATION> | container element for a semantic annotation in an XML format | None |
The use of content rather than presentation tagging for mathematics is sometimes referred to as "semantic tagging" [Buswell 1996]. The parse-tree of a fully bracketed MathML content tagged element structure corresponds directly to the expression-tree of the underlying mathematical expression. We therefore regard the content tagging itself as encoding the syntax of the mathematical expression. This is, in general, sufficient to obtain some rendering and even some symbolic manipulation (e.g., polynomial factorization).
However, even in such apparently simple expressions as X + Y, some additional information may be required for applications such as computer algebra. Are X and Y integers,or functions, etc.? 'Plus' represents addition over which field? This additional information is referred to as Semantic Mapping. In MathML, this mapping is provided by the SEMANTICS, ANNOTATION and XML-ANNOTATION elements.
The SEMANTICS element is the container element for the MathML expression together with its semantic mapping. SEMANTICS expects a variable number three child elements. The first is the element (which may itself be a complex element structure) for which this additional semantic information is being defined. The second and subsequent children, if any, are instances of the elements ANNOTATION or XML-ANNOTATION.
The SEMANTICS tags also accepts a "SEMTYPE" attribute for use by external processing applications. One use might be a URL for a semantic context dictionary, for example. Since the semantic mapping information might in some cases be provided entirely by the "SEMTYPE" attribute, the ANNOTATION or XML-ANNOTATION elements are optional.
The ANNOTATION element is a container for arbitrary data. This data may be in the form of text, computer algebra encodings, C programs, or whatever a processing application expects. ANNOTATION has an attribute ENCODING defining the form in use. Note that the content model of ANNOTATION is #PCDATA, so care must be taken that the particular encoding does not conflict with XML parsing rules.
The XML-ANNOTATION element is a container for semantic information in well-formed XML. For example, an XML form of the OpenMath semantics could be given. Another possible use here is to embed, for example, the presentation tag form of a construct given in content tag form in the first child element of SEMANTICS (or vice versa). ANNOTATION has an attribute ENCODING defining the form in use.
For Example:
<SEMANTICS>
<EXPR> <MN>123</MN> <OVER/>
<MN>456</MN> </EXPR>
<ANNOTATION encoding="Mathematica">
N[123/456, 39]
</ANNOTATION>
<ANNOTATION encoding="TeX">
$0.269736842105263157894736842105263157894\ldots$
</ANNOTATION>
<XML-ANNOTATION encoding="MathML-Presentation">
<MROW>
<MN> 0.269736842105263157894 </MN>
<MOVER>
<MN> 736842105263157894 </MN>
<MO> &horizontalLine; </MO>
</MOVER>
</MROW>
</XML-ANNOTATION>
<XML-ANNOTATION encoding="OpenMath">
<OM_APP>..</OM_APP>
</XML-ANNOTATION>
</SEMANTICS>
where <OM_APP>..</OM_APP> are the elements
defining the additional semantic information.
Of course, providing an explicit semantic mapping at all is optional, and in general would only be provided where there is some requirement to process or manipulate the underlying mathematics.
Although semantic mappings can easily be provided by various proprietary, or highly specialized encodings, there are no widely available, non-proprietary standard semantic mapping schemes. In part to address this need, the goal of the OpenMath effort is to provide a platform-independent, vendor-neutral standard for the exchange of mathematical objects between applications. Such mathematical objects include semantic mapping information. The OpenMath group has defined an SGML syntax for the encoding of this information [OpenMath, 1996]. This element set could provide the basis of one XML-ANNOTATION element set.
An attraction of this mechanism is that the OpenMath syntax is specified in SGML, so that the whole expression is checkable by a DTD-based parser.
In order to facilitate compatibility with Cascading Style Sheets (CSS1), all MathML elements accept CLASS and STYLE attributes. At present, many MathML properties that would be desirable to control via style sheets are not defined in CSS1. Conversely, CSS1 properties which are applicable to MathML may not be accessible to embedded MathML renderers in the immediate future. However, the CLASS and STYLE attributes provide some degree of compatibility now, and may provide much greater compatibility in the future.
There is a great deal of work underway on the problem of controlling the layout of XML extensions to HTML via style sheet mechanisms. The HTML-Math working group will be coordinating its efforts with other groups over the next year to insure that MathML will be compatible with emerging style sheet mechanisms.
Content or semantic tagging goes along with the (frequently implicit) premise that, if you know the semantics, you can always work out a presentation form. When an author's main goal is to mark up re-usable, evaluatable mathematical expressions, the exact rendering of the expression is probably not critical, provided that it is easily understandable. However, when an author's goal is more along the lines of providing enough additional semantic information to make a document more accessible by facilitating better visual rendering, voice rendering, or specialized processing, controlling the exact notation used becomes more of an issue.
MathML elementss accept an attribute OTHER (see 7.2.4) which can be used to specify things not specifically documented in MathML. On content tags, this attribute can be used by an author to express a preference between equivalent forms for a particular content element construct, where the selection of the presentation has nothing to do with the semantics. Examples might be
Thus, if a particular renderer recognized a display attribute to select between script style and display style fractions, an author might write
to indicate that the rendering 1/x is preferred.<EXPR OTHER='display="scriptstyle"'><MN> 1 </MN><OVER/><MI> x </MI></EXPR>
The information provided in the "OTHER" attribute is intended for use by specific renderers or processors, and therefore, the permitted values are determined by the renderer being used. It is legal for a renderer to ignore this information. This might be intentional, in the case of a publisher imposing a house style, or simply because the renderer does not understand them, or is unable to carry them out.
There will be a need for the construction of translators for the layout of material tagged with content tags according to the wishes of those wanting the output.