Working Draft 10-Jun-97
1. Introduction
1.1 Mathematics and its Notation
A distinguishing feature of mathematics is the use of a complex and highly
evolved system of two-dimensional symbolic notations. As J. R. Pierce has
written in his book on communication theory, mathematics and its notations
should not be viewed as one and the same thing [Pierce
1961]. Mathematical ideas exist independently of the notations that
represent them. However, the relation between meaning and notation is subtle,
and part of the power of mathematics to describe and analyze derives from
its ability to represent and manipulate ideas in symbolic form. The challenge
in putting math on the Web is to capture both notation and content in such
a way that documents can utilize both the highly-evolved notational practices
of print, and the emerging capabilities of the new electronic medium.
Mathematical notations are constantly evolving as people continue to
discover innovative ways of approaching and expressing ideas. Even the
commonplace notations of arithmetic have gone through an amazing variety
of styles, including many defunct ones advocated by leading mathematical
figures of their day [Cajori 1928/1929].
Modern mathematical notation is the product of centuries of refinement,
and the notational conventions for high-quality typesetting are quite complicated.
For example, at the simplest level, variables, or letters which stand for
numbers, are usually typeset today in a special italic font subtly distinct
from the text italic, and the spacing around the symbols +, -, x and /
is slightly different from that of text, to reflect that by convention
multiplication is a higher precedence operation than addition. Slightly
more sophisticated is the now common convention of keeping the baselines
of superscripts and subscripts aligned in formulas although the base letters
may have different heights and depths; in addition, parentheses around
subformulas are usually made to grow with the sizes of the expressions
they enclose, or to make clearer the grouping within a mathematical expression.
Many subfields of mathematics have their own refined notational devices
too.
Although notational conventions in mathematics, and printed text in
general, can be complicated, they guide the eye and make printed expressions
much easier to read and understand. Though we usually take them for granted,
we rely on hundreds of conventions such as paragraphs, capital letters,
font families and cases, and even the device of decimal-like numbering
of sections such as we are using in this document (an invention due to
G. Peano, who is probably better known for his axioms for the natural numbers).
It is easy to forget how important these aids to comprehension are until
one is obliged to read a poorly typeset document. This is apparent in many
mathematical documents on the Web today, where there are difficulties in
properly displaying even the most basic notations; we must substitute an
"x" for a times symbol, and use a slash for the division sign.
However, there is more to putting math on the Web than merely finding
ways of displaying traditional mathematical notation in a Web browser.
The Web represents a fundamental change in the underlying metaphor for
knowledge storage, a change in which interconnectivity plays a central
role. It is becoming increasingly important to find ways of communicating
mathematics which facilitate automatic processing, searching and indexing,
and reuse in other mathematical applications and contexts. With this advance
in communication technology, there is once again an opportunity to expand
our ability to represent, encode, and ultimately to communicate our mathematical
insights and understanding with each other. We believe that MathML is an
important step in developing Mathematics on the Web.
1.2 Origins and Goals
1.2.1 The History of MathML
The problem of encoding mathematics for computer processing or electronic
communication is much older than the Web. The common practice among scientists
before the Web was to write papers in some encoded form based on the ASCII
character set, and e-mail them to each other. Several markup methods for
mathematics, in particular TeX, were already in wide use in 1992, just
before the Web rose to prominence, [Poppelier,
van Herwijnen and Rowley 1992]
Since its inception, the Web has demonstrated itself to be a very effective
method of making information available to widely separated groups of individuals.
However, even though the World Wide Web was initially conceived and implemented
by scientists for scientists, the capability to include mathematical expressions
in HTML is very limited. At present, most mathematics on the Web consists
of text with GIF images of scientific notation, which are difficult to
read and author.
The World Wide Web Consortium (W3C) has long recognized that lack of
support for scientific communication is a serious problem, and Dave Raggett,
the author of the HTML 3.0 working draft, made a proposal for HTML Math
in 1994. Following a panel discussion on math at the WWW IV Conference
in Darmstadt in April 1995, a group was formed to discuss the problem further.
In the intervening two years, this group has grown, and been formally reconstituted
as the W3C HTML-Math working group.
The MathML proposal reflects the interests and expertise of a very diverse
group. Many contributions to the development of MathML deserve special
mention, some of which we touch on here. One such contribution concerns
the question of accessibility, especially for the visually handicapped.
T. V. Raman is particularly notable in this regard. Neil Soiffer and Bruce
Smith from Wolfram Research shared their extensive experience with the
problems of representing mathematics in connection with the design of Mathematica
3.0. MathML has benefited from the participation of a number of working
group members involved in other math encoding efforts in the SGML community,
including Stephen Buswell from Stilo, Stéphane Dalmas from INRIA,
Stan Devitt from Waterloo Maple, Angel Diaz, Robert Sutor, and Stephen
Watt from IBM. In particular, MathML has been influenced by the OpenMath
project, the work of the ISO 12083 working group, and Stilo Technologies'
work on a 'semantic' math DTD fragment. Finally, the American Mathematical
Society has played a key role in the development of MathML. Among other
things, it has provided two working group chairs: Ron Whitney led the group
from May 1996 to March 1997, and Patrick Ion, who has co-chaired the group
with Robert Miner from The Geometry Center, from March 1997 to the present.
1.2.2 The Need for MathML
The demand for effective means of electronic scientific communication is
high. Increasingly, researchers, scientists, engineers, educators, students
and technicians find themselves working at a distance and relying on electronic
communication. At the same time, the image-based methods that are currently
the predominant means of transmitting scientific notation over the Web
are primitive and inadequate. Document quality is poor, authoring is difficult,
and the mathematical content of notation is not available for searching,
indexing, or reuse in other applications.
The most obvious problems with HTML for mathematical communication are
of two types:
Display Problems. Consider the equation 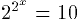 .
This equation is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or for other
font sizes, the equation is too small or too large. A second point to observe
is that the equation image was generated against a white background. Thus,
if a reader or browser resets the page background to the gray default,
the anti-aliasing is wrong. Next, consider the equation
.
This equation is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or for other
font sizes, the equation is too small or too large. A second point to observe
is that the equation image was generated against a white background. Thus,
if a reader or browser resets the page background to the gray default,
the anti-aliasing is wrong. Next, consider the equation 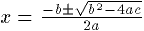 .
This equation has a descender which places the baseline for the equation
at a point about a third of the way from the bottom of the image. One can
pad the image like this:
.
This equation has a descender which places the baseline for the equation
at a point about a third of the way from the bottom of the image. One can
pad the image like this: 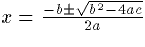 ,
so that the centerline of the image and the baseline of the equation coincide,
but this causes problems with the inter-line spacing, which also makes
the equation difficult to read. Moreover, center alignment of images is
handled in slightly different ways by different browsers, making it impossible
to guarantee proper alignment for different clients.
,
so that the centerline of the image and the baseline of the equation coincide,
but this causes problems with the inter-line spacing, which also makes
the equation difficult to read. Moreover, center alignment of images is
handled in slightly different ways by different browsers, making it impossible
to guarantee proper alignment for different clients.
Image-based equations are generally harder to see, read and comprehend
than the surrounding text in the browser window. Moreover, these problems
become worse when the document is printed. The resolution of the equations
will be around 70 dots per inch, while the surrounding text will typically
be 300 or more dots per inch. The disparity in quality is judged to be
unacceptable by most people.
Encoding Problems. Consider trying to search this page for part
of an equation, for example, the "=10" from the first equation above. In
a similar vein, consider trying to cut and paste an equation into another
application. Using image based methods, neither of these common needs can
be adequately addressed. Although the use of ALT text in the document source
can help, it is clear that highly interactive Web documents must provide
a more sophisticated interface between browsers and mathematical notation.
Another problem with encoding mathematics as images is that it requires
more bandwidth. By using markup-based encoding, more of the rendering process
is moved to the client machine. Markup describing an equation is typically
much smaller than an image of the equation.
Some of the display problems associated with including math notation
as images could be solved by improving browser image handling. However,
even if image handling in browsers were improved, the encoding problems
would still remain. In planning for the future, it is clear that making
the information contained in mathematical expressions conveniently accessible
to other applications will be increasingly important.
1.2.3 The Uses of MathML
In order to fully integrate mathematical content into web documents, and
to address the current shortcomings of HTML, we cannot merely upgrade image-based
methods. Instead, we need a better method of encoding mathematical notation
and content for the Web.The design of such an encoding must take into account
the needs it must meet. A dominant consideration, therefore, in the design
of MathML has been the diversity of ways in which the broader scientific
community needs to use math on the Web.
The education community is a large and important group that must be
able to put scientific curriculum materials on the Web. At the same time,
educators often have limited resources of time and equipment, and are severely
hampered by the difficulty of authoring technical Web documents. Teachers,
for example, need to be able to post notes and exams quickly and easily.
Electronic textbooks are another way of using the Web which will potentially
be very important in education. Management consultant Peter Drucker has
recently been prophesying the end of big-campus residential higher education
and its distribution over the Web [Drucker
1997]. The form of an electronic text will need to be active, allowing
links to other scientific software and graphics.
In the research community here are more and more large, online knowledge
bases as typified by highly successful preprint servers, like that at Los
Alamos started by Paul Ginsparg. This is especially true in some areas
of physics and mathematics where academic journal prices have been increasing
at an unsustainable rate. In mathematics there are large collections at
Duke, MSRI and SISSA, and on the AMS e-MATH server. In addition, databases
of information on mathematical research, such as Mathematical Reviews and
Zentralblatt für Mathematik, offer millions of records containing
math on the Web. In addition, any design for math on the Web must facilitate
the maintenance and operation of large document collections, where automatic
searching and indexing are important. Because of the large collection of
legacy data, especially TeX documents, the ability to convert between existing
formats and new formats is also very important to the research community.
Corporate and academic scientists and engineers also use technical documents
in their work to collaborate, to record results of experiments and computer
simulations, and to verify calculations. For such uses, math on the Web
must provide a standard way of sharing information that can be easily read
and generated by authors and by software.
Another design requirement is the ability to render mathematical material
in other media such as speech or braille, which is extremely important
for the visually impaired.
Commercial publishers are also involved with math on the Web at all
levels from electronic versions of print books to interactive textbooks
to academic journals. Publishers require a method of putting math on the
Web that is capable of high-quality output, robust enough for large-scale
commercial use, and preferably compatible with their current, usually SGML-based,
production systems.
1.2.4 Design Goals of MathML
In order to meet the diverse needs of the scientific community, the
HTML-Math Working Group intends to develop an open specification for a
mathematical markup language, MathML, to be used with HTML, that:
-
Is suitable for teaching, and scientific communication.
-
Is easy to learn and to edit by hand for basic math notation, such as arithmetic,
polynomials and rational functions, trigonometric expressions, univariate
calculus, sequences and series, and simple matrices.
-
Is well suited to template and other math editing techniques.
-
Insofar as possible, allows conversion to and from other math formats,
both presentational and semantic, such as TeX and computer algebra systems.
Output formats may include graphical displays, speech synthesizers, computer
algebra systems input, other math layout languages such as TeX, plain text
displays (e.g. VT100 emulators), and print media, including braille. It
is recognized that conversion to and from other notational systems or media
may lose information in the process.
-
Allows the passing of information intended for specific renderers.
-
Supports efficient browsing for lengthy expressions.
-
Provides for extensibility, for example through contexts, macros, new rendering
schemas or new symbols. Some extensions may necessitate the use of new
renderers.
These goals focus largely on the encoding problem for mathematics on the
Web. At the same time, it is clear that in order to be useful, MathML software
must be implemented. To this end, the Working Group has identified a short
list of additional implementation goals for MathML. These goals arose
from a great deal of experimentation, and attempt to describe concisely
the minimal functionality required for MathML to be fully implemented.
-
MathML equations in HTML pages should render properly in popular Web browsers,
in accordance with reader and author viewing preferences, and at the highest
quality possible given the capabilities of the platform.
-
HTML documents containing MathML equations should print properly and at
high-quality printer resolutions.
-
MathML equations in Web pages should be able to react to mouse gestures,
and coordinate communication with other applications through the browser.
-
Equation editors and converters should be developed to facilitate the creation
of Web pages containing MathML equations.
The Working Group believes that all of these goals are attainable in the
near term by using embedded elements such as Java applets, plug-ins and
ActiveX controls to render MathML. However, the extent to which these goals
are met depends on the cooperation and support of browser vendors, and
other software developers. The HTML Math working group has been encouraged
by the willingness to try to accommodate the needs of math which the Document
Object Model Working Group of the World Wide Web Consortium has shown.
1.3 The Role of MathML on the Web
1.3.1 Layered Design of Mathematical Web Services
Considering the diverse demands placed on MathML by the potential users
of math on the Web, it is clear MathML has to be a very powerful system
if it is to meet its goals addressing their needs. It must be flexible
and extensible, capable of producing very high-quality rendering, and it
must provide a sophisticated interface to external software. Unfortunately,
any markup language that encodes enough information to do all these tasks
well will of necessity involve some complexity.
At the same time, it is important for many groups, such as students,
to have simple ways to include math in Web pages by hand. Similarly, other
groups, such as the TeX community, would be best served by a system which
allowed the direct entry of markup languages like TeX directly in Web pages.
In order to resolve the contradictory goals of providing more specialized
kinds of input and output for specific user communities, while still providing
a system of sufficient generality and power, the idea of a layered design
architecture naturally emerges.
MathML is designed to be a general and powerful underlying communication
layer which is machine-friendly. It is designed to encode complex notational
and semantic structure in an explicit, regular, and easy to process way.
Sitting on top of the MathML communication layer will be input syntax layers
that are designed to be simple to learn, and easy to edit by hand. Many
different input syntax layers designed for different user communities can
potentially all piggy-back on top of the MathML layer. Equation editors
and translators will be used to convert input syntaxes into MathML. Alternatively,
renderers may convert input syntaxes directly included in Web pages into
MathML on the fly.
One consequence of a layered design architecture is that the core language
of MathML is not intended to be particularly well-suited to hand entry.
Instead, MathML is designed to facilitate the development of software and
input syntaxes that are carefully tailored to the needs of specific user
communities, while providing a low-level, standardized format for communication
over the Web.
In some ways, MathML is analogous to other low-level, communication
formats such as TeX's DVI format, or Adobe's PostScript. You can create
a PostScript file in a variety of ways, depending on your needs; experts
write and modify them by hand, authors create them with word processors,
graphic artists with paint programs, and so on. Once you have a PostScript
file, however, you can share it with a very large audience, since devices
which render PostScript, such as printers and screen previewers, are widely
available.
Similarly, the HTML-Math working group envisions typical users creating
MathML documents by using equation editors, converters or other scientific
software, or by hand in some cases, according to their needs. A student
might prefer to use a menu-driven equation editor that can write out MathML
to an HTML file. A researcher might use a computer algebra package that
automatically encodes the mathematical content of an expression, so that
it can be cut from a Web page and evaluated by a colleague. A journal publisher
might typically use a program that converts TeX markup to MathML. Others
may prefer to include other math markup languages directly in an HTML page
which is translated on the fly into MathML by a specific embedded renderer
in a Web browser. Regardless of the method used to create a MathML web
page, once it exists, all the advantages of a powerful and general communication
layer become available. MathML-compliant renderers can be developed for
a variety of purposes including speech, print, embedded web software, and
computer algebra. One may expect that eventually MathML can be integrated
into other arenas where mathematical formulas occur, such as spreadsheets, statistical
packages and engineering tools.
The HTML-Math working group is moving aggressively to ensure that both
MathML software and high-level input syntax layers will soon be available.
The Working Group plans to produce a proposal for input syntax and macro
capability by May, 1998. One proposed short
form input syntax has already been developed by Wolfram Research. In
addition, two renderers, WebEQ
and IBM techexplorer,
have announced plans to implement MathML, and both will accept an input
syntax based on TeX. In addition, a number of software vendors and other
organizations have expressed interest in developing MathML-compliant software,
including the American Mathematical Association, IBM, members of the OpenMath
consortium, Geometry Technologies, Stilo Technologies, Waterloo Maple,
and Wolfram Research.
1.3.2 Relation to Other Web Technology
Part of the reason for designing MathML as a low-level communication layer
is to stimulate mathematical Web software development. MathML provides
a way of coordinating the development of modular authoring tools and rendering
software. By making it easier to develop a functional piece of a larger
system, MathML can stimulate a "critical mass" of software development,
greatly to the benefit of potential users of math on the Web.
However, in order to effectively stimulate software development, it
is important that MathML interact well with existing software. In particular,
MathML has been designed with three kinds of interaction in mind: with
existing mathematical markup languages, with HTML extension mechanisms,
and with Web browser extension mechanisms.
Existing Mathematical Markup Languages
Without question, one of the greatest influences on mathematical markup
languages of the last two decades is the TeX typesetting system developed
by Donald Knuth. TeX is a de facto standard in the mathematical research
community, and it is pervasive in the scientific community at large. TeX
sets a standard for quality of visual rendering, and a great deal of effort
has gone into insuring MathML can provide the same visual rendering quality.
Moreover, because of the large body of legacy documents in TeX, and because
of the large authoring community versed in TeX, a priority in the design
of MathML was the ability to convert TeX math input into MathML format.
Extensive work on encoding mathematics has also been done in the SGML
community, and SGML-based encoding schemes are widely used by commercial
publishers. ISO 12083 is an important layout-based markup language which
primarily describes the visual presentation of mathematical notation. Because
ISO12083 and its derivatives share many presentational aspects with TeX,
and because SGML enforces structure and regularity more than TeX, much
of the work in ensuring MathML is compatible with TeX also applies well
to ISO12083.
MathML also pays particular attention to compatibility with other mathematical
software, and in particular, computer algebra systems. Many of the presentation
elements of MathML are derived in part from the mechanism of typesetting
boxes. The MathML content elements are heavily indebted to the OpenMath
project and the Semantic Maths DTD. The OpenMath project has close ties
to both the SGML and computer algebra communities, and has laid a foundation
for an SGML-based means of communication between mathematical software
packages, among other things.
HTML Extension Mechanisms
In addition to harmonizing well with the established traditions in mathematical
markup, MathML must harmonize with the existing HTML environment. This
problem is not unique to MathML. The success of HTML has led to enormous
pressure to incorporate a wide variety of data types and software applications
into the Web. Each new format or application potentially places new demands
on HTML, and on browser vendors. In response, a simplified dialect of SGML
called XML (Extensible Markup Language) is being developed.
One of the goals of XML is to be suitable for use on the Web, and in
the context of this discussion it can be viewed as a general mechanism
for extending HTML. As its name implies, extensibility is a key feature
of XML; authors are free to declare and use new tags and attributes. At
the same time, the XML syntax carefully enforces document structure to
facilitate automatic processing and maintenance of large document collections.
In addition to its advantages, XML has garnered support from major browser
vendors as well. Consequently, both on theoretical and pragmatic grounds,
it makes a great deal of sense to specify MathML as an XML application,
and we have done so.
Browser Extension Mechanisms
While XML provides a powerful and flexible way of specifying the structure
and syntax of MathML, a mechanism is also required for specifying how MathML
should be processed and rendered. Ideally, browsers should natively process
and display MathML, and it is not unreasonable to think this will ultimately
be the case. However, in the near term, it will be necessary to provide
interim methods for displaying and processing MathML.
A general model for rendering and processing XML extensions to HTML
is still being developed by the W3C XML working group. However, broad features
of the model are already fairly clear. Style sheets provide the mechanism
for specifying the processing model, and embedded objects provide a way
of doing the processing. Cascading Style Sheets (CSS)
and DSSSL are the
main style specification mechanism under consideration, and some combination
of these methods will probably be used to bind rendering instructions to
XML extensions of HTML.
At present, however, the rendering and style parameters that are recognized
by major browsers are geared toward primarily text-based content. Thus,
for content such as MathML (or many other kinds of complex structured data)
it is necessary to extend native browser capabilities by providing embedded
elements to do the rendering. As one popular slogan puts it, XML gives
Java something to do. Ultimately, some sort of style sheet mechanism will
instruct a browser to use a particular embedded renderer to process MathML
and coordinate the resulting output with the surrounding Web page. In order
to achieve this kind of full nteraction, however, it will be necessary
to define a document object model rich enough to facilitate complicated
interactions between browsers and embedded elements. For this reason, the
HTML-Math working group is coordinating its efforts closely with the Document
Object Model working group.
While work on XML, style sheets, embedded objects, and the document
object model is still ongoing, the intent of these efforts is to provide
an infrastructure capable of supporting sophisticated markup and rendering
applications such as MathML. Moreover, while much remains to be done, enough
of this infrastructure is already available to provide a workable, short
term solution for the needs of MathML.
1.4 Encoding Notation and Content Structure
The fundamental challenge in defining a mathematics markup language for
the Web is reconciling the need to encode both the presentation of a mathematical
notation and the content of the mathematical idea or object which it represents.
The relationship between a mathematical notation and a mathematical
idea is subtle and deep. On a formal level, the results of mathematical
logic raise profound and unsettling questions about the correspondence
between symbolic logic systems and the phenomena they model. At a more
intuitive level, anyone who uses mathematical notation knows the difference
that a good choice of notation can make; the symbolic structure of the
notation suggests the logical structure. For example, the Leibniz notation
for derivatives "suggests" the chain rule of calculus through the symbolic
cancellation of fractions:
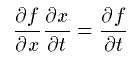
Mathematicians and teachers understand this very well; part of their
expertise lies in choosing notation that emphasizes key aspects of a problem
while hiding or diminishing extraneous aspects. It is commonplace in math
and science to write one thing when technically something else is meant,
because long experience shows this actually communicates the idea better
at some higher level.
At the same time, mathematical notation is capable of prodigious rigor.
Used carefully, mathematical notation is virtually free of ambiguity. Even
when mathematical notation is "abused" in the way described in the preceding
paragraph, a completely precise description of the underlying idea still
usually exists. Of course in practice, the more abstract the subject matter,
the more difficult and tedious it becomes to give a full description of
the concepts under discussion; typically the context is understood between
the author and the audience, and notation is used almost as shorthand.
In many other settings, though, the full, precise meaning of mathematical
expressions is apparent to both the author and the reader. Moreover, there
is great utility in encoding that precise meaning explicitly in the markup
language so that it is available for use by other renderers and processors,
from computer algebra systems to voice renderers or even 3D graphics packages.
Given the complex relationship between mathematical notation and ideas,
between authors and readers, and the multiplicity of scenarios in which
they interact, the question remains, "What should the content of a mathematical
markup language for the Web be?" The answer which MathML gives is this:
MathML is a markup language for describing the notational
structure and mathematical content of mathematical expressions.
In some situations, the mathematical content of an expression may be little
more than the symbolic structure of the notation. For these situations,
MathML provides tags for all commonly used mathematical notational schema,
such as <MSUP>, <MFRAC> and <MROW>, used to indicate superscripts,
fractions, and horizontal rows of symbols respectively. There are roughly
25 of these presentation tags with around 40 attributes.
In terms of their ability to describe high quality screen and print
rendering, the MathML presentation tags are on a par with TeX. More importantly,
because the tags describe notational structure, not visual layout per se,
the presentation expression structure is as compatible as possible with
the natural underlying mathematical structure.
Consider the notation 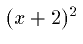 .
Using MathML presentation tags, this might be marked up as:
.
Using MathML presentation tags, this might be marked up as:
<MSUP>
<MROW>
<MF>(</MF>
<MROW>
<MI>x</MI>
<MO>+</MO>
<MN>2</MN>
</MROW>
<MF>)</MF>
</MROW>
<MN>2</MN>
</MSUP>
Note that the superscript schema contains two subexpressions corresponding
to the base (an MROW element) and exponent (an MN element), reflecting
the natural mathematical structure of the exponentiation operation with
two arguments that the notation represents. Moreover, the MathML syntax
reinforces the tendency to attach a superscript to the logical base. This
contrasts sharply with a presentational markup language like TeX where
by default the superscript is attached only to the final parenthesis.
Although a superscript can denote function composition, a derivative,
or even a cohomological index, a human reader easily understands from the
context that the superscript in the preceding example usually indicates
a power. However, making this information explicit facilitates speech rendering
and other automatic processing. Ideally, it should be easy to specify simple
mathematical operations completely enough to aid speech rendering, etc.,
and in MathML it is. MathML provides around 50 content tags in addition
to the presentation tags. Using these tags, the preceding example can be
encoded as
<EXPR>
<EXPR>
<MI>x</MI>
<PLUS/>
<MN>2</MN>
</EXPR>
<POWER/>
<MN>2</MN>
</EXPR>
Note we do not need to encode the parentheses to specify the meaning, since
the scoping is defined by the EXPR elements. However, in order to specify
that parentheses should be displayed, one would typically mix presentation
and content markup, using the "fence" presentation element <MF> as shown
below:
<EXPR>
<EXPR>
<MF>(</MF>
<MI>x</MI>
<PLUS/>
<MN>2</MN>
<MF>)</MF>
</EXPR>
<POWER/>
<MN>2</MN>
</EXPR>
The MathML content tags more or less cover elementary mathematics through
basic calculus. It is worth noting that HTML-Math working group expects
to provide extension mechanisms to MathML for describing the content of
very advanced mathematics as well. However, by mixing the presentation
and content tags from the MathML core standard, a great deal of commonly
used mathematics can be expressed in a relatively unambiguous way. In a
situation demanding completely rigorous content specification, such as
communication between scientific software packages, an encoding system
such as OpenMath is more suitable. In many other situations, processors
such as voice renderers and computer algebra systems could use heuristic
methods to infer much more of the intended mathematical context than is
possible from presentational markup alone.
In cases where the semantic meaning of an expression cannot be unambiguously
described with MathML tags, there is a way of binding arbitrary semantic
interpretation data and presentation structure together. The author is
free to provide semantic data in any form, for example as an OpenMath expression,
or a computer algebra system expression. This makes the information available
for renderers and processors that know how to take advantage of it, while
providing a notation for screen and print renderings.
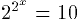 .
This equation is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or for other
font sizes, the equation is too small or too large. A second point to observe
is that the equation image was generated against a white background. Thus,
if a reader or browser resets the page background to the gray default,
the anti-aliasing is wrong. Next, consider the equation
.
This equation is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or for other
font sizes, the equation is too small or too large. A second point to observe
is that the equation image was generated against a white background. Thus,
if a reader or browser resets the page background to the gray default,
the anti-aliasing is wrong. Next, consider the equation 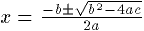 .
This equation has a descender which places the baseline for the equation
at a point about a third of the way from the bottom of the image. One can
pad the image like this:
.
This equation has a descender which places the baseline for the equation
at a point about a third of the way from the bottom of the image. One can
pad the image like this: 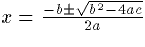 ,
so that the centerline of the image and the baseline of the equation coincide,
but this causes problems with the inter-line spacing, which also makes
the equation difficult to read. Moreover, center alignment of images is
handled in slightly different ways by different browsers, making it impossible
to guarantee proper alignment for different clients.
,
so that the centerline of the image and the baseline of the equation coincide,
but this causes problems with the inter-line spacing, which also makes
the equation difficult to read. Moreover, center alignment of images is
handled in slightly different ways by different browsers, making it impossible
to guarantee proper alignment for different clients.
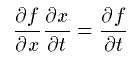
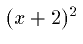 .
Using MathML presentation tags, this might be marked up as:
.
Using MathML presentation tags, this might be marked up as: