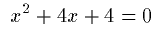
This section introduces the basic features of MathML markup. It gives a number of examples of basic MathML expressions, introducing the use of presentation tags, content tags, and mixed markup.
The intention of this section is to give a brief overview of how MathML works in practice. It is not intended as a full tutorial, or a reference, but merely as a way of rapidly conveying some of the possibilities of MathML.
One way of using MathML is to use presentation tags to describe the expression structure of mathematical notation. Here are some simple examples:
Notation: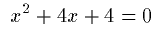
Markup:
<MROW>
<MROW>
<MSUP>
<MI>x</MI>
<MN>2</MN>
</MSUP>
<MO>+</MO>
<MROW>
<MN>4</MN>
<MO>⁢</MO>
<MI>x</MI>
</MROW>
<MO>+</MO>
<MN>4</MN>
</MROW>
<MO>=</MO>
<MN>0</MN>
</MROW>
There are two important things to note here. The first is that there are two kinds of MathML tags -- those that contain data like MI, MN and MO, and those that only contain other nested MathML tags like MSUP and MROW. The second is the use of nested MROWs to denote terms, in this case the left-hand side of the equation functioning as an operand of "=". Typing data and marking terms greatly facilitate things like spacing for visual rendering, voice rendering, line breaking, as well as automatic processing by external applications.
The tags that contain data declare the type of the data. For example, the MI tag indicates an identifier, or variable, while the MN tag indicates a number. All of the type tags have two-letter names.
The other tags denote layout schema like scripts, fractions or rows. In general each schema must contain a prescribed number of subexpressions in a specific order. The MSUP schema, for example, expects exactly two subexpressions, of which the first is the base, and the second is the script.
Notation: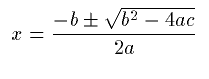
Markup:
<MROW>
<MI>x</MI>
<MO>=</MO>
<MFRAC>
<MROW>
<MROW>
<MO>-</MO>
<MI>b</MI>
</MROW>
<MO>±</MO>
<SQRT>
<MROW>
<MSUP>
<MI>b</MI>
<MN>2</MN>
</MSUP>
<MO>-</MO>
<MROW>
<MN>4</MN>
<MO>⁢</MO>
<MI>a</MI>
<MO>⁢</MO>
<MI>c</MI>
<MROW>
</MROW>
</SQRT>
</MROW>
<MROW>
<MN>2</MN>
<MO>⁢</MO>
<MI>a</MI>
</MROW>
</MFRAC>
</MROW>
Notice that the plus/minus sign is a special named entity. MathML provides a very comprehensive list of entity names for mathematical symbols. In addition to the mathematical symbols needed for screen and print rendering, MathML provides symbols to facilitate audio rendering. For audio rendering, it is important to be able to automatically determine whether
<MROW>
<MI>z</MI>
<MROW>
<MF>(</MF>
<MROW>
<MI>x</MI>
<MO>+</MO>
<MI>y</MI>
</MROW>
<MF>)</MF>
</MROW>
</MROW>
means "z times the quantity x plus y" or "z of x plus y". The entities ⁢ and ⁡ provide a way for authors to directly encode the distinction for audio renderers. For instance in the first case ⁢ should be inserted after the line containing the z. MathML also introduces entities like ⅆ which represents a "differential d" which renders with slightly different spacing in print, and is usually rendered as "with respect to" in speech. Unless content tags or some other mechanism are used to eliminate the ambiguity, authors should always use these entities, in order to make their documents more accessible.
Notation: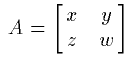
Markup:
<MROW>
<MI>A</MI>
<MO>=</MO>
<MROW>
<MF>[</MF>
<MTABLE>
<MTR>
<MTD><MI>x</MI></MTD>
<MTD><MI>y</MI></MTD>
</MTR>
<MTR>
<MTD><MI>z</MI></MTD>
<MTD><MI>w</MI></MTD>
</MTR>
</MTABLE>
<MF>]</MF>
</MROW>
</MROW>
This example introduces several more schema, including the MF fence tags. Most schema have a number of attributes that control the details of their screen and print rendering. For example, there are around half a dozen attributes for fence schema that control whether a fence should stretch at all, whether it should stretch symmetrically, and so on. The attributes for entities are set to default values determined by a dictionary. The W3C HTML Math working group plans to release a proposal for a standard MathML dictionary by September, 1997. (See appendix C.)
Notation: 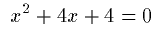
Markup:
<EXPR>
<EXPR>
<EXPR>
<MI>x</MI>
<POWER/>
<MN>2</MN>
</EXPR>
<PLUS/>
<EXPR>
<MN>4</MN>
<TIMES/>
<MI>x</MI>
</EXPR>
<PLUS/>
<MN>4</MN>
</EXPR>
<E/>
<MN>0</MN>
</EXPR>
Note that MathML content tags are typically contained within an EXPR
schema. The EXPR schema denotes a semantically meaningful expression.
Although MathML syntax does not prohibit EXPR tags from containing
purely notational presentation markup, as a convention, authors should
only use EXPR tags when the contents have an unambiguous mathematical
meaning.
Another important feature of the MathML content tags is that many of them are empty tags. Note that in XML, an empty tag is of the form < ... />. Many of the empty content tags play the role of standard infix operators. To make the order of operations explicit, and to determine the scope of certain operators, the EXPR tags function like parentheses.
The MathML content tags cover a range of basic math objects and operators. However, it will frequently be the case that the content tags cannot fully describe even relatively simple mathematical expressions. In these situations, authors are free to mix content and presentation tags as in the following example, in which the MSQRT schema is used, and the ± enitity is marked as an operator token.
Notation: 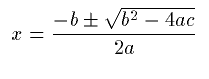
<EXPR>
<MI>x</MI>
<E/>
<EXPR>
<EXPR>
<EXPR>
<MO>-</MO>
<MI>b</MI>
</EXPR>
<MO>±</MO>
<MSQRT>
<EXPR>
<EXPR>
<MI>b</MI>
<POWER/>
<MN>2</MN>
</EXPR>
<MINUS/>
<EXPR>
<MN>4</MN>
<TIMES/>
<MI>a</MI>
</TIMES>
<MI>c</MI>
</EXPR>
</EXPR>
</MSQRT>
</EXPR>
<OVER/>
<EXPR>
<MN>2</MN>
<TIMES/>
<MI>a</MI>
</EXPR>
</EXPR>
</EXPR>
Although mixing presentation and content tags provides an easy way of giving a relatively unambiguous coding of moderately complicated content, there are situations where this strategy is unsatisfactory. In the preceding example, the author has indicated that the denominator of the fraction is "2 times a". However, the author has no explicit control over how a particular renderer represents the operator "times" on the screen. Typically, it will just be rendered as juxtaposition of symbols, but if the author wants it to be rendered with a multiplication sign, another MathML construction is required.
The W3C HTML Math Working group plans to make a proposal specifying an extension mechanism for MathML which provides authors with a way of specifying how a content tag should render using style sheets. However, situations will still remain where an author needs a way of directly specifying presentation markup, while also providing additional semantic information directly to specific renderers. An example might consist of presentation mark up for a function together with additional data intended for displaying its graph in a 3D graphics environment.
For these situations, MathML provides the SEMANTICS tag:
Notation: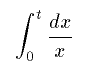
Markup:
<SEMANTICS>
<MROW>
<MSUBSUP>
<MO>∫</MO>
<MN>0</MN>
<MI>t</MI>
</MSUBSUP>
<MFRAC>
<MROW>
<MO>ⅆ</MO>
<MI>x</MI>
</MROW>
<MI>x</MI>
</MFRAC>
</MROW>
<EXPR>
<INT>
<LOWLIMIT>
<MN>0</MN>
</LOWLIMIT>
<UPLIMIT>
<MI>t</MI>
</UPLIMIT>
<EXPR>
<MN>1</MN>
<OVER/>
<MI>x</MI>
</EXPR>
<BVAR>x</BVAR>
</INT>
</EXPR>
</SEMANTICS>
The SEMANTICS tag expects two children. The first child consists of presentation markup. The second child can contain arbitrary semantic markup. In this example, the second child is composed of MathML content tags. However, in principle, the second child could be an OpenMath expression, a computer algebra expression, or even a C program. An attribute of the SEMANTICS element can be used to specify the type of encoding.